Edwin Hubble, in his efforts to do for galactic morphology what Darwin did for animal taxonomy, first classified spirals according to the tightness of the windings observed: Sa for the most tightly wound systems to Sc for galaxies with wide-flung arms. SBa, etc, were used to denote spirals with strong bars. Over the years the classification scheme has become, like many schemes in astronomy, complex and cumbersome. There are now 'SBbc (peculiar)' galaxies and others even more strange. The suffix 'd' has been added for galaxies with even looser flung arms than Sc-type. There are exceptions and shades of grey in every parameter.
The origins and very natures of spiral arms has been a slippery problem. The initial and obvious theory is that the stars are simply arranged in a spiral pattern. Among the original pioneers of the field was Bertil Lindblad who worked on spiral structure steadily from 1927 through 1965 (Binney and Tremaine 94, hereafter BT94). Lindblad realized that the naive idea of stars arranged permanently in spirals was untenable due to the winding problem. Since galactic disks rotate differentially over most of their surface (as evidenced by the characteristic flat rotation curves observed spectroscopically), a radial line objects (a spoke) will quickly become curved as the galaxy rotates. However, as the inner particles revolve faster than those at the edge, the spoke will quickly become wrapped around the galaxy in an increasingly tight spiral. Clearly this winding problem calls for more sophisticated solutions to the structure of spiral arms. Any material spiral arms would last a few galactic years (complete revolutions of the galaxy at some radius) at most.
In the 1950's it was thought that magnetic fields could be the mysterious generators of spiral structure. However, the mechanism for how this would work was never clearly developed. Furthermore, one would expect that, if magnetic fields were behind the density organizations, the energy density of the fields would be equivalent to that of the mass gravitational energy. Subsequent observations of field strength showed it falling short by a factor of five (BT94). It is known, however, that magnetic fields follow the path of spiral arms.
The first really robust theory was developed by C. C. Lin and Frank Shu in papers of 1964 and 1966. They proposed that spiral arms were the manifestations of spiral density waves in the gas and stars of a galaxy. This theory, or variations on it, seems to be the most resilient even today.
In §2 I will discuss some of the theoretical basis for density waves in rotating disks including resonances and traveling waves. The concept of wave amplification will be discussed from two different approaches. In §3 I will give an overview of some of the observational criteria which provide constraints for modeling and in §4 discuss some models for the generation of spiral density waves. Finally I will mention some of the competing theories of spiral structure generation.
Discussion of spiral density waves cannot proceed without some background in the theory of differentially rotating disks. When working with such a system, it is desirable to use a rotating coordinate frame which revolves at some speed ![]() . For an axisymmetric disk with a flat rotation curve (a good first order approximation to the disk of a spiral galaxy), this rotation speed
. For an axisymmetric disk with a flat rotation curve (a good first order approximation to the disk of a spiral galaxy), this rotation speed ![]() will match up with the rotation speed at some radius
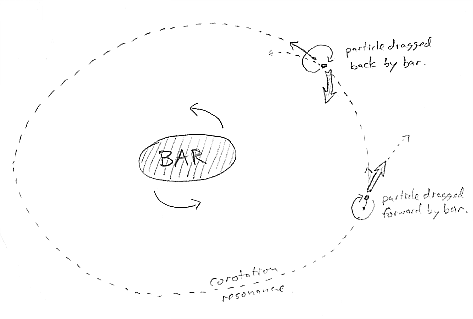
will match up with the rotation speed at some radius ![]() (R). Particles inside this radius will appear to revolve in the direction of the frame rotation (prograde) while outside this corotation radius, they will be retrograde.
(R). Particles inside this radius will appear to revolve in the direction of the frame rotation (prograde) while outside this corotation radius, they will be retrograde.
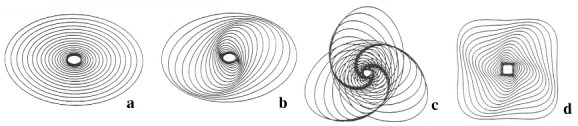
Since we are specifying a rotating frame, orbits for which ratio of epicyclic frequency to orbital frequency are irrational can be made to close by appropriate choice of ![]() . For a mass which completes two radial oscillations while performing one complete azimuthal trip in the rotating frame, we get elliptical orbits with the center at the center of the potential. Similarly, a ratio of 3/2 gives a three-armed cloverleaf pattern. If we align a number of these 2/1 orbits concentrically and populate them with stars, we see that a bar is formed (figure 1). This is particularly effective in the inner, rigidly rotating portions of a disk where the whole bar will rotate as a unit. Furthermore, by giving each successive concentric orbit a slight azimuthal offset, a spiral pattern can be formed. Clearly when the majority of the stars are arranged in these spiral or bar patterns, the mass asymmetry will begin to affect the overall potential.
. For a mass which completes two radial oscillations while performing one complete azimuthal trip in the rotating frame, we get elliptical orbits with the center at the center of the potential. Similarly, a ratio of 3/2 gives a three-armed cloverleaf pattern. If we align a number of these 2/1 orbits concentrically and populate them with stars, we see that a bar is formed (figure 1). This is particularly effective in the inner, rigidly rotating portions of a disk where the whole bar will rotate as a unit. Furthermore, by giving each successive concentric orbit a slight azimuthal offset, a spiral pattern can be formed. Clearly when the majority of the stars are arranged in these spiral or bar patterns, the mass asymmetry will begin to affect the overall potential.
If we perturb the axisymmetric potential of the rotating disk with a small non-axisymmetric component as above, it makes sense to define the rotation speed of that perturbation as the frame speed; thus we define the pattern speed ![]() . This potential is m-fold symmetric and may arise from a central bar pattern (m=2) as discussed above, an triaxial dark halo (m=2), some external perturbing agent such as a companion galaxy (m=1), or from large local mass concentrations within the disk of the galaxy (m=many). We will assume that particles move in epicyclic orbits with epicyclic frequency (Goldreich 87)
. This potential is m-fold symmetric and may arise from a central bar pattern (m=2) as discussed above, an triaxial dark halo (m=2), some external perturbing agent such as a companion galaxy (m=1), or from large local mass concentrations within the disk of the galaxy (m=many). We will assume that particles move in epicyclic orbits with epicyclic frequency (Goldreich 87)
![]()
where ![]() is the azimuthal frequency.
is the azimuthal frequency.
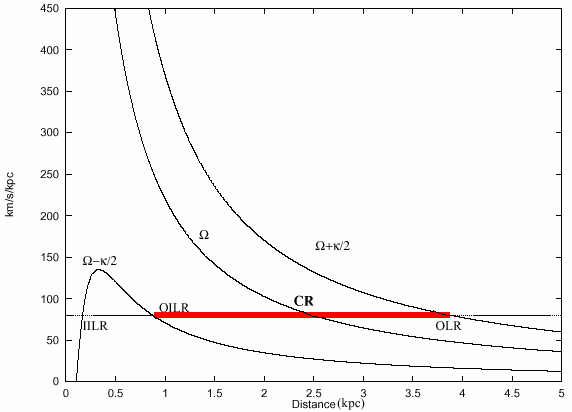
Two other resonances, discovered by and named after Lindblad lie interior and exterior to the CR. These are the locations where ![]() and are roughly equivalent to Kirkwood resonances seen in the Asteroid belt due to Jupiter's perturbing force on the symmetric solar field. Again take a particle orbiting with m=2. If at the Inner Lindblad Resonance (ILR) it is at the top of its epicycle when the end of the bar swings by below it, it will be at the top of its next epicycle when the opposite end of the bar swings by. The particle is oscillating radially at an integral multiple of the driving frequency and at a constant phase (Kormendy and Norman 79) which represents a condition of forced oscillation-another barrier in the effective potential. Figure 3 shows a plot of
and are roughly equivalent to Kirkwood resonances seen in the Asteroid belt due to Jupiter's perturbing force on the symmetric solar field. Again take a particle orbiting with m=2. If at the Inner Lindblad Resonance (ILR) it is at the top of its epicycle when the end of the bar swings by below it, it will be at the top of its next epicycle when the opposite end of the bar swings by. The particle is oscillating radially at an integral multiple of the driving frequency and at a constant phase (Kormendy and Norman 79) which represents a condition of forced oscillation-another barrier in the effective potential. Figure 3 shows a plot of ![]() versus various resonant frequencies as a function of radius for a typical galaxy.
versus various resonant frequencies as a function of radius for a typical galaxy.
The Outer Lindblad Resonance (OLR) is similar except that particles are moving relatively retrograde from the rotating bar. Both resonances present barriers to the radial potential profile in the disk. Waves tend to propagate through the disk in these annular regions between resonances.
Kormendy and Norman (1979) point out that not all galaxies have inner Lindblad radii. The necessary conditions for the formation of an ILR are a relatively rapid transition from a region of solid-body rotation to one of differential rotation (e.g. a flat rotation curve). Galaxies in which the transition is gradual enough or where ![]() for a large radius may lack ILRs entirely. The implications of this will be discussed below.
for a large radius may lack ILRs entirely. The implications of this will be discussed below.
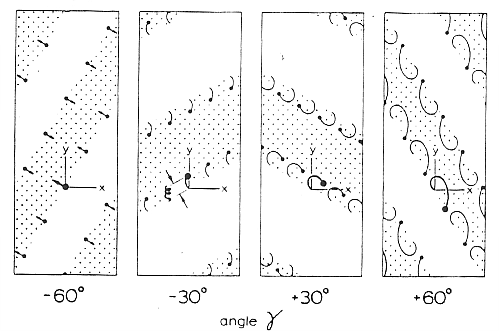
Take a portion of a density wave composed of two rows of particles (one at the inner and one at the outer edge) (figure 4). The spiral is inclined at an angle of ![]() degrees to the radial direction (a leading wave). Self gravity pulls the two rows of particles together, but coriolis forces act on the inner, leading row pushing them inward and on the outer, trailing row pushing them outward in epicyclic motion. Meanwhile sections of arm at greater radii are orbitting slower than those at lesser radii (differential rotation) and the leading arm starts to tilt or unwind. The particles continue in their coriolis-induced (shear) paths as the arm tilts in the same sense. Though the shear paths lead the particles out of a non-rotating arm after a full rotation, the continuing change in wave inclination keeps moving the arm boundary away from the circulating particles. Thus each particle contributes more to the self-gravity of the arm than they otherwise would by a factor of
degrees to the radial direction (a leading wave). Self gravity pulls the two rows of particles together, but coriolis forces act on the inner, leading row pushing them inward and on the outer, trailing row pushing them outward in epicyclic motion. Meanwhile sections of arm at greater radii are orbitting slower than those at lesser radii (differential rotation) and the leading arm starts to tilt or unwind. The particles continue in their coriolis-induced (shear) paths as the arm tilts in the same sense. Though the shear paths lead the particles out of a non-rotating arm after a full rotation, the continuing change in wave inclination keeps moving the arm boundary away from the circulating particles. Thus each particle contributes more to the self-gravity of the arm than they otherwise would by a factor of ![]() . For an arm tilt from -60
. For an arm tilt from -60 ![]() to +60
to +60 ![]() , this is a boost of 156% (Toomre 81). The additional self-gravity leads to higher density and higher total mass as neighboring ambient particles are attracted. So swing amplification acts to both amplify the wave and change it from leading to trailing.
, this is a boost of 156% (Toomre 81). The additional self-gravity leads to higher density and higher total mass as neighboring ambient particles are attracted. So swing amplification acts to both amplify the wave and change it from leading to trailing.
Trailing waves are not swing amplified in the manner described above. However, in the case of a galaxy without an ILR (as discussed by Kormendy and Norman 1979), it is easy to turn an inward-propagating trailing wave (for instance from a recent swing amplification at the CR) into an outward propagating leading wave by sending it across a chord of the inner disk of the galaxy and out the other side. This is illustrated schematically in BT94 (figure 6.20). The leading wave would then be amplified, turned into a trailing wave and again sent back across leading to a tremendous positive feedback loop.
![]()
which describes the relative strength of the corotation barrier. A large X value implies a high potential barrier which is more efficient at reflecting waves. Goldreich (1987) shows that the reflected and transmitted waves are related to the incident wave as follows
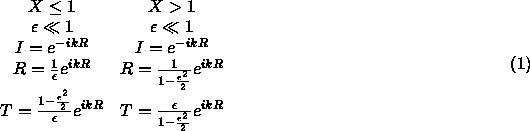
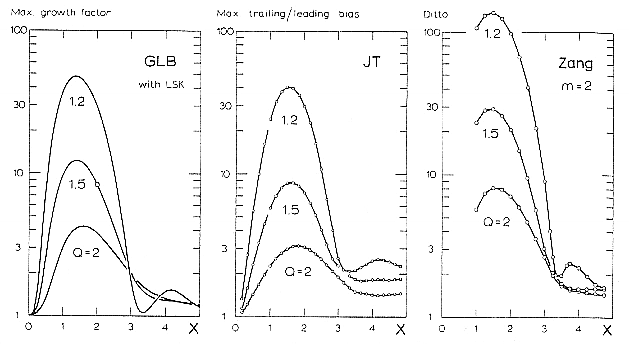
where ![]() is a small parameter. Notice the change in sign of k on reflection in both cases. The results of three different numerical analyses are summarized in figure 5 showing the effects of the parameters Q and X on the gain of a wave. Maximum gain is roughly 10 depending on Q (Toomre 81).
is a small parameter. Notice the change in sign of k on reflection in both cases. The results of three different numerical analyses are summarized in figure 5 showing the effects of the parameters Q and X on the gain of a wave. Maximum gain is roughly 10 depending on Q (Toomre 81).
One final effect we can see in the parameter X is that it is inversely proportional to m. Higher m numbers should be selected for stronger amplification. However, radius range in which waves can propagate-between the inner and outer Lindblad resonances goes as ![]() , selecting for lower m values. The optimal symmetry for a propagating wave seems to be m
, selecting for lower m values. The optimal symmetry for a propagating wave seems to be m ![]() 2 (BT94) explaining why two armed spirals are most prevalent.
2 (BT94) explaining why two armed spirals are most prevalent.
We should probably take a moment to discuss some observations by which models of spiral arm formation will be judged. The first major distinction between galaxies is that between the Grand Design and Flocculent spirals. Any theory must account for both types and all the range in between. Grand designs (such as M81 and M51) typically have two large, contrasty arms with sparse inter-arm regions. The arms typically span roughly a full 360 degrees or more in angular extent. There is usually an inner disk separated from the outer and the major arms by a ring of material. It's unclear whether this ring is a manifestation of a Lindblad resonance or actually a very tightly wound spiral (Yuan and Kuo 98).
Most grand design spirals and indeed most spirals in general have a two armed structure. These arms are almost always trailing in nature. There are a few cases of three armed galaxies and leading arms. Andromeda, for instance appears to have two trailing arms and one leading one! NGC 3675 and 4378 appear to have only one arm each. The Milky Way appears to have several distinct systems of arms (see below). Never-the-less, any theory needs to account for a preference for two trailing arms.
Flocculent spirals on the other end of the spectrum usually have no single arm that can be traced for more than 30 degrees around the disk. Typically there are many arms and portions of arms scattered throughout the disk. With recent observations, many previous flocculents have been discovered to have weak spiral patterns in the near IR. The distinction between the two seems to be the surface density of gas. NGC 5055, the cannonical flocculent galaxy-recently seen to have a weak two-arm structure-displays only about one fifth as much gas as the grand design M51 (Thornley and Mundy, 97).
Spiral structure is clearly not just an optical effect. Evidence is provided by the wide range of wavebands which show the same general structure. HI and IR observations confirm that arms are the highest concentrations of gas and dust and thus it makes sense that these would be areas of star formation. We know from observations of stellar polarization and pular faraday rotation in our own galaxy that magnetic fields often follow the paths of spiral arms. Indeed the spiral arms are narrowest in B band illuminated by hot, young stars. R band shows the arms to be broader which meshes with the increased spatial and velocity dispertion among older, cooler stars. Since most stars by both number and mass are K and M type, this pattern in the red means that a significant portion of the mass is participating in the spiral structure (BT94).
Another observational distinction is bars. Many galaxies have them; some do not. Yet galaxies of both types exhibit spiral structure. Kormendy and Norman (1979) studied the 54 spirals which, at that time, had observed rotation curves. They found that strong spiral patterns were often, but not always linked to central bars or to massive companions. Subsequent observations have shown that many galaxies previously thought to be lacking bars in fact do contain small bars or some sort of central oval distortion.
The major uncertainty regarding spiral arms is their timescale. Without historical perspective, we know very little about the permanance of galactic structures. Perhaps grand design spirals are transitory and, given a few galactic ``years'', M81 and its grand fellows will evolve into amorphous, ragged spirals with little structure. We also know very little about the formation and evolution through Hubble Time of spiral galaxies, though the Hubble Deep Field and future observations with both HST and NGST will undoubtedly help clear up this issue.
This detonation wave theory would explain why arms appear thinner and more contrasty in young stars than in the older population; also the concentrations of gas and dust along the arms and the relatively rarefied interarm medium. This picture appears quite plausible for small, irregular systems such as the LMC and for spurs and filamentary features in larger galaxies (Norman, 82), but there is no reason to believe that two symmetric and opposite waves of star formation would be occuring at the same time. Grand design spirals are not generated.
Lin and Shu's hypothesis of steady-state spirals only well-describes grand design spirals and breaks down at the ragged spiral end of the scale. These may well be fit better by a smaller scale chaotic theory of spiral formation. In this type of theory small, chaotic perturbations on the local scale (less than a kiloparsec typically) will collapse into structures which will then be sheared out into spiral structures. This theory relies critically on the temperature dependence of Q, the stability parameter (BT 94). As velocity dispersion increases, the system moves toward a more unstable situation. When the density is high enough and star formation occurs, these stars start with very little initial velocity dispertion, thus pulling Q back up and restabilizing the local region.
Observations seem to back this theory. Since the 1979 Kormandy and Norman paper, quite a large percent of spirals appear to have either bar or bar-like structures at their cores or have had recent interactions with companion galaxies.
The Milky Way is now thought to contain a small bar at the center based on COBE, IRAS and radio observations of CO. Cloud velocities exhibit a strong east-west asymmetry near the core (Binney et. al. 1992; others). There are a system of spiral arms at roughly the solar radius as well as at least one arm system interior to these. This 3kpc arm does not appear to have a companion (m=1) and may be caused by an asymmetrical bar with a 5% perturbation to the galactic field and a pattern speed of 169km/sec/kpc (Yuan, 92).
Martin Weinberg (1992) summarizes the observations of Liszt and Burton (1980) of a triaxial massive halo around our galaxy with a pattern speed of 6km/sec/kpc, quadrupole strength of 2% galactic, and lag position of -45 ![]() relative to the sun. This perturbation would place the ILR at about 11kpc, outside the local standard of rest.
relative to the sun. This perturbation would place the ILR at about 11kpc, outside the local standard of rest.
Weinberg continues by hypothesizing a bar consistent with the findings of Liszt and Burton (1980) with a quadrupole strength less than 40% leading the LSR by 45 ![]() . This system would put the CR at roughly 3kpc and the OLR at 5-6kpc. Stellar kinematics observations are inconclusive at this time.
. This system would put the CR at roughly 3kpc and the OLR at 5-6kpc. Stellar kinematics observations are inconclusive at this time.
A great deal of work has been done on spiral structure since the early work of Lindblad. While it seems density waves are a very efficient way to form arms, there appear to be more than one way to skin a galactic cat. While some theories such as MHD have been pretty conclusively discounted, the strengths of those still in the running are complimentary and may explain different facets of the problem. Stochastic star formation and chaotic theory seem to explain smaller-scale structure well while global modes and driven systems are more coherent over the larger scale. Observations of our own galaxy suggest that many or all of these systems are at work to one degree or another.
Bertin, G., in Athanassoula, E. ed., Internal Kinematics and Dynamics of Galaxies, IAU Symposium No. 100, 119-120, 1983.
Binney, J. and Gerhard, O., in Holt, S.S. and Verter, F., eds, Back to the Galaxy, AIP Conference Proceedings 278. 1992.
Binney, J., and Tremaine, S., Galactic Dynamics, Princeton Series in Astrophysics, 1994.
Goldreich, P, in Fang Li Zhi, ed., Origin, Structure and Evolution of Galaxies, Beijing, 127-143, 1987.
Kormandy, J., and Norman, C.A., 1979, ApJ, 233:539-552.
Lin, C.C., in Athanassoula, E. ed., Internal Kinematics and Dynamics of Galaxies, IAU Symposium No. 100, 117-118, 1983.
Liszt, H.S. and Burton, W.B. 1980 ApJ, 236, 779.
Mihalas, D. and Routly, P.M., Galactic Astronomy, W. H. Freeman and Company, San Francisco, 1968.
Norman, C.A., in Athanassoula, E. ed., Internal Kinematics and Dynamics of Galaxies, IAU Symposium No. 100, 163-174, 1983.
Thornley, M.D. and Mundy, L.G, 1997, ApJ 484:202-221.
Toomre, A. (1981), in The Structure and Evolution of Normal Galaxies, eds. Fall, S.M. and Lynden-Bell, D. (Cambridge University Press, London). 111-136.
Weinberg, M.D. in Holt, S.S. and Verter, F., eds, Back to the Galaxy, AIP Conference Proceedings 278. 1992.
Yuan, C., in Holt, S.S. and Verter, F., eds, Back to the Galaxy, AIP Conference Proceedings 278. 1992.
Yuan, C., and Kuo, C., 1997, ApJ 486:750-762.
Yuan, C., and Kuo, C., 1998, ApJ 497:689-698.
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html spiral.tex.
The translation was initiated by Charles Danforth on Mon Mar 6 15:10:48 EST 2000