Problem Set 6

ASTR 3730

Read Chapters 15, 17, 18

1. Imagine that a star only 1pc from Earth goes supernova and achieves a luminosity of 10¹¹ solar luminosities.
a) What is the flux at Earth in ergs/cm²/s?
b) By what factor is the flux on the Earth's surface increased over that from the Sun alone?
c) What will be the temperature of the Earth when it reaches a new thermal equilibrium?
d) Would life on Earth survive?
e) How distant would the supernova have to be if the temperature on the Earth is to remain below 140F?
f) Assuming the density of stars in the galaxy is 0.1 per cubic parsec, there are 10¹¹ stars in the galaxy, and there is one supernova every 30 years, how often would a supernova that raises T above 140F occur?
g) Severe high energy radiation would hit the Earth if the supernova were within 20pc. How often does this happen?

2. Neutron Stars
a) A marshmallow weighing 5 gm is dropped from a large height onto a 1 solar mass neutron star. How much energy is released when it impacts the surface? How does this compare with a nuclear bomb?
b) In Larry Niven's famous story Neutron Star the hero does a close orbit around a neutron star while hanging on for dear life. How long does a close orbit around a neutron star last? Is the story accurate from a physics point of view?
c) Tidal force on an object can be computed by taking the difference of gravitational attraction between the front and the back of an object. Estimate the tidal force on our hero. Can he survive?

3. Black Holes
The x-ray star Cygnus X-1 is the only serious candidate we have for a black hole. In the visible one observes the primary star to be an O9 supergiant (M=24M_¤ , R=16R_¤ ). By observing the absorption lines in the atmosphere of the primary we know that the binary period is 5.6 days and that the orbital velocity of the primary is about 85km/sec.
a) Assume the orbit is circular. What is the radius (r) of the primary's orbit around the center of mass of the system?
b) What is the semi-major axis (a) in terms of the masses of the primary (M), the secondary (m), and r ?
c) Use Kepler's Law to derive a relation between m and m+M, r, and P (the period).
d) As an approximation assume M+m=M=24M_¤ . What is m? Why is this not a neutron star?
e) What is the radius of the black hole?
d) The x-ray emission is seen to randomly flicker on a timescale of one millisecond. Explain this.

4. Calculate the moment of inertia of a neutron star (I=2MR²/5). Calculate the energy of spin of the Crab Pulsar (E=Iw²/2) where the period is 0.033 seconds. The Crab is slowing at a rate that will stop its spin in 2500 years. Calculate its power lost.

5. The acceleration g of a freely falling body near a black hole is given by:

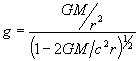
Show that far from the event horizon this reduces to the usual Newtonian form.  Show the force becomes infinite at the event horizon.

6. Let dt¥ be the time interval elapsed for an observer at infinity. The elapsed time for a local observer is:

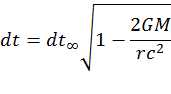
Show that a local observer far from the black hole ages at the same rate as the observer at infinity, and that as the local observer approaches the event horizon aging stops as observed from infinity.

7. A particle falling from infinity takes time

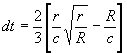to fall from radius r to the event horizon at radius R.   Calculate dt for a particle falling from 10km onto a one solar mass black hole.

8. Using:

as derived by Hawking, calculate the evaporation timescale for a one solar mass black hole.