Magnitudes
Archaic: very conveninient if
a) no calculations
b) all stellar objects are blackbodies 3 - 10000 K (i.e. stars)
c) use only photography in visual
But still in use
Take a star (alpha centuri): call it m=0
Take another star 100x fainter: call it m=5
Take another star 104xfainter: call it m=10
Algorithm for stars of same type as alpha centuri
1) Take number of times fainter I0/I
2) Take log10(I0/I)
3) Multiply by 2.5
exponential to the 2.51 power 2.51=
What happens is spectrus not the same
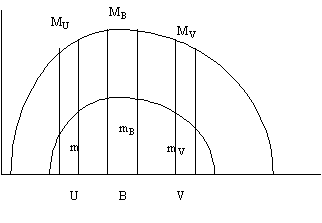
Three standard magnitudes
color excess
MU, MB, MV scaled for standard star
Could just quote flux densities at the 3 points
magnitudes very misleading is bulk of flux is outside optical
Sun 26.5 Faintest visible 6
Full Moon 13 Faintest Detectable 22
Sirius 1.5
Absolute Magnitude (M)
m=M at 10 pc
m at d
m at 10 
but m = -log2.51 Id = 
M = -log2.51 I10
M - m = -2.5 log Id + 2.5 log I10
= -2.5 log (
)
= -2.5 log (
)2
= -5 log d + 5 log 10
M = m - 5 log d + 5
Astrophysical Plasma
-Cosmic/Solar abundances
What does it emit in various circumstances
If we understand shysics then we can deduce circumstances of the matter
All photons are generated by the acceleration of charged particles
Will start with the simplest case:
Isolated charge
Larmor Formula
Relativistic Form:
(for colinear acceleration and velocity)
(for perpendicular acceleration and velocity)
We thus know the power here, but not the spectru. It gets complicates and E & M not appropriate here
Qualitative approach:
To become a photon electric field must be perturbed so that 
can add
vt
then we can get a photon
if goes through many cycles then integral will be zero
Therefore, wt < 1 for photon creation
n
c
Conservation of energy predicts a result like this. You can’t put more energy into a photon than is lost from a particle.
What can cause acceleration of a particle?
Collisions with other particles
à Bremsstrahlung Radiation
E & B Fields
E fields get shorted out
B fields à Synchrotron and Cyclotron Radiation
Collisions between particles and particles spiralling in B fields account for virtually all orgination of photons
Optically thin à photons escape as generated
Optically Grey or Thick à photons interact with other matter before escaping
We will now discuss emission mechanisms Synchrotron and Bremsstrahlung in optically thin case
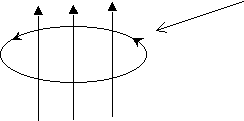
Cyclotron Radiation
B
v
Non-relativistic particle
Velocity = v
Mass = m
Therefore, cutoff at wc
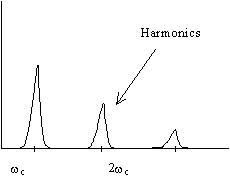
With ensembles of particles: lines are not perfect d function
Widened by:
change in w (relativistic effect)
collisional broadening
self absorption
plasma distortion
non uniform B
but, 
therefore, 
How does a particle behave in such a field?
note: photon loses energy 106 times slower à electrons are source
but 
let 
Therefore, 
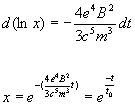
loses energy on a timescale
/B2 = 10years/B2guess
Radiates at 
Hz = 2.8 B MHz
Synchrotron Radiation
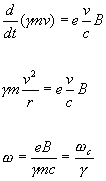
Because of relativistic effects synchrotron does not radiate at fundamental frequency
In instantaneous rest from Larmor formula
Emits radiation at what particle thinks cyclotron frequency is, goes around at 
but due to time, emits at wc in its frame, but sees Brest = g Bobs emits at gwc
Transform à 
Main Output at 
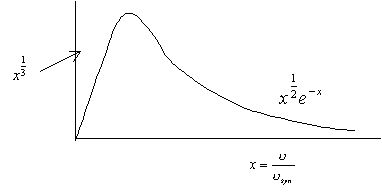
described exactly as modified Bessel function
Ensemble of Electrons
Power law distribution of energy
convolve functions
jn = emissivity per unit volume
à Power law spectrum is seen
Synchrotron Decay Time
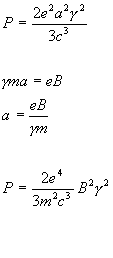
P= 1.6 * 10-15 B2g2 ergs/s
E= gmc2 =0.91*10–27 * 9*1020 g ergs
E=8.2*10-7 g ergs
sec
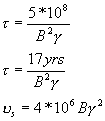solve for B & g
Example:
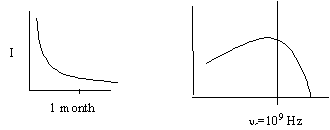
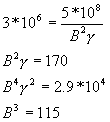
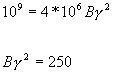
therefore,
B ~ 5 gauss
g ~ 7