Optically Thick Case

Radiative Transfer

Until now:

But what if absorption occours?

But what if it gets very thick?

Then dIn = 0

Let us look at this more closely.

Consider the particles doing the absorbing and emitting.

Take two states upper, U, and lower, L.

Separate them by EU - EL = hn

Then Boltzman tells us:

also, in equilibrium

AUL = spontaneous emission

InBUL = stimulated emission

NLBLUIn = absorption

combine

let T --> infinity, therefore I --> infinity

then

So in general, in equilibrium

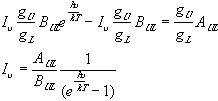
Can be shown using box normalization and quantum mechanics that (in most circustances)

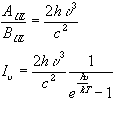Blackbody radiation erg cm-2 s-1 Hz-1 st

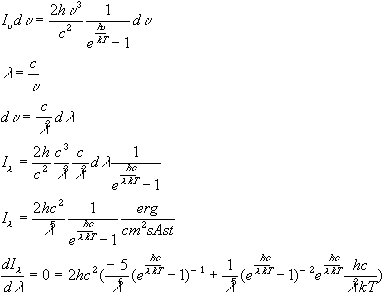
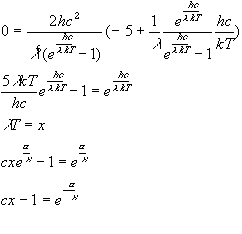
Wien Law A*K

Remember, sun: T=5000

lm=5000

lT = 25*106

Next look at low n end hn << kT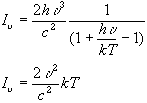

Rayleigh-Jeans law

Can’t measure T if Area unknown very inconvient if hn = kT region hidden

 

Finally -- total emission

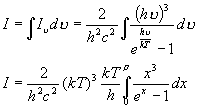
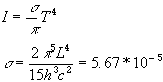
From a flat dA

 

 

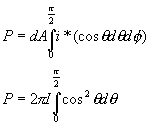
Review

Basic

 

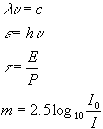
Radiation from a charge

 

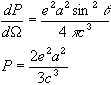
Cyclotron

 

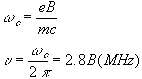
Synchrotron

 

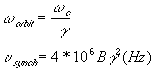
Bremsstrahlung

 

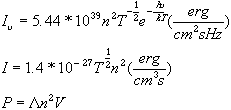
Compton Scattering

 

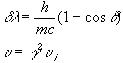
Blackbody

 

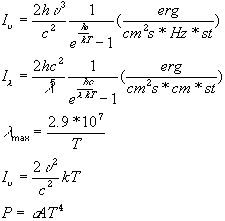
Sun is a star

Star is a ball of gas with an energy source in the middle

Chemical Energy

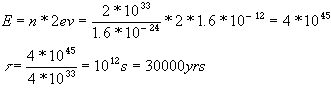
Gravitational Energy

 

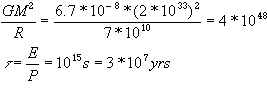
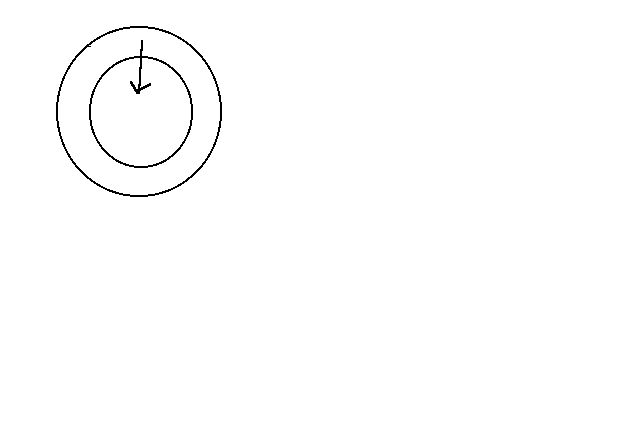
Nuclear 1MeV per particle instead of 2eV

E = 5 * 105 * 4 * 1045 = 2 * 1051 ergs

t = 15 * 109 years -- very close to correct!

What is the theral timescale of the Sun?

Thermal content at core 106K

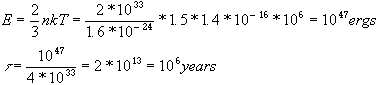
Takes 106 years to change significantly

Lets make a star

Ball of gas at mass M

Collapses Gravitationally

For a few thousand years chemical processes have an effect (very short time)

Gravity holds it together

Thermal Pressure holds it up

Balance the two and you have a star

P = nkT ideal gas law

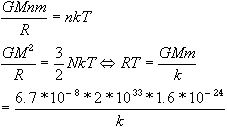
RT=1.5*1018 cm deg

Chemical energy dissipates 1000 years

Gravitational energy dissipates in 3*107 years

Keeps contracting until nuclear burning sets in at T=15 million

Equilibrium is achieved

If R decreases then T increases

If T increases L increases

If L increases T increases more

If T increases R increases

Stable equilibrium is achieved